The main motivation for this project was to examine the inter-connectedness of wikipedia articles. We used a dataset produced by Stanford that modeled wikipedia articles as nodes in a
graph and the links between articles as edges. We implemented Dijkstra, Stoer-Wagner, and Breadth First Search to analyze the dataset. We also
created visualizations using a barebones graphics library. This project was completed using C++ and the repository can be accessed here.
Dijkstras' Algorithm
Dijkstras algorithm is a simple shortest path algorithm that we used to examine optimal distances between articles.
Ultimately, we created two functions for the purpose of our analysis. One returned an integer representing the
shortest path weight and the other returned a vector containing the path actually traversed between the two nodes.
For the purpose of our work, the latter function (returning a vector), proved to be of far more sustinence, although
the conclusions of both were ultimately transitively explanatory of each other as illustrated in the conclusion.
Minimum Links Traversed
This used the int function of dijkstras and was helpful in explaining the sheer level of connectivity throughout the
nodes of the graph. For example, a short traversal from an article title Viking to one titled Glass encountered a
staggering 181 links on its path of only 4 nodes.
Shortest Node Path
This used the vector function of dijkstras and was remarkable for understanding just how easy it was to connect any
article in the graph. We hypothesized needing large traversals of 20+ nodes to connect seemingly unrelated topics but
our findings put connectivity distance into a new astounding perspective. We found that we were able to connect
(arbitrarily) unrelated articles with a path of no greater than 5 nodes .
Stoer-Wagner
Our primary idea behind utilizing Stoer-Wagner in our analysis was to be able to find to minimum cut edges that
could potentially illustrate the most signifigant links in the entire graph. We hoped that this finding would
allude to especially important articles that played a massive role in connecting a vast number of other articles.
Our Shortcoming
We fell short of achieving our goal in using this algorithm on our dataset due to a simple oversight in its actual
runtime. Our implementation of Stoer-Wagner's minimum cut algorithm has a runtime of O(|V|^3), which isn't a daunting
runtime on a graph of around 100 nodes persay. However, our graph's primary connected component contains over 4000
nodes, which means that Stoer-Wagner would have taken over 64,000,000,000 (64 billion!) iterations to complete. Our
virtual machine was simply not cut out for this task, and as a result, we felt short of actually being able to use it in
the work of our analysis.
Breadth First Search
We used BFS as a means to understand underlying connectivity by measuring the size of the graph's components. It didn't play a role in helping us see how individual pages connected to others, but rather, served as a tool to see the span of connections starting from any one specific article. Our results were substantial, and we found that of the 4604 nodes in our dataset, 4588 were found to be in a single connected component.
Visualization
On top of the three algorithms, we created gifs and images to visualize our findings. Unfortunately,
we weren't able to include as many nodes in our traversals as we would have liked to due to limitations in our
machines and the size of the dataset. As shown further below, we had to limit it to only 100 nodes.
Here's what the degree of South America looks like. Note the radius of each drawn node is based off its degree.

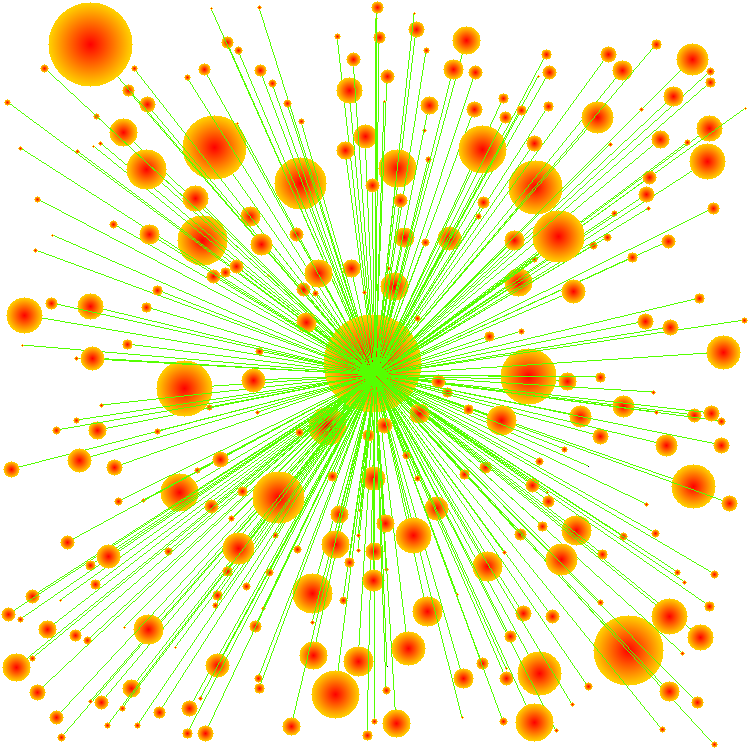
This is what the traversal of the first 100 nodes of BFS starting on Zulu looks like:
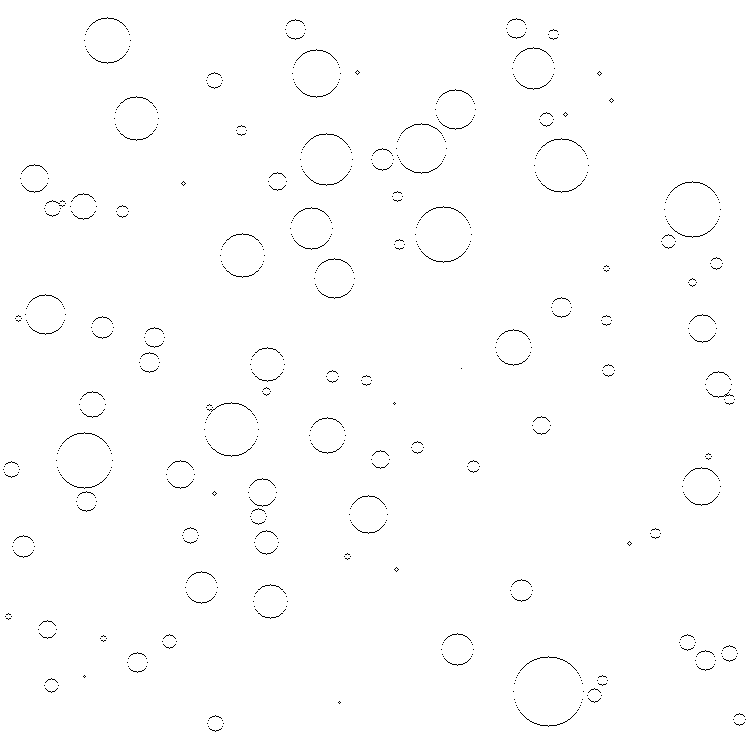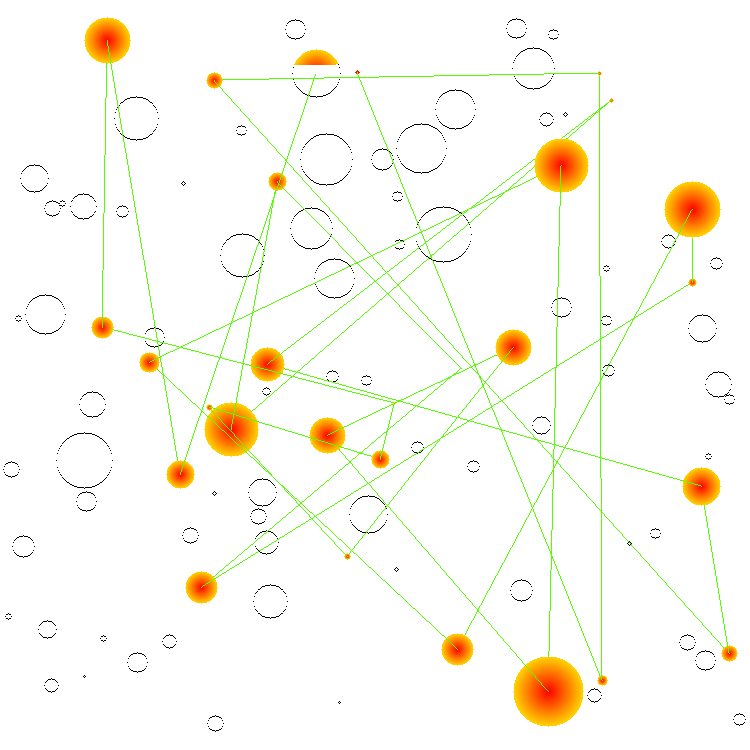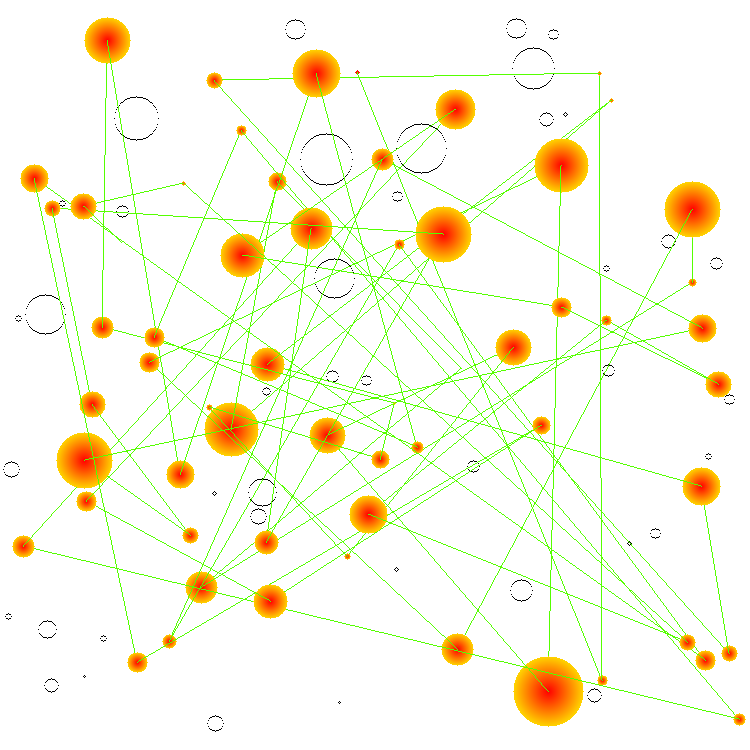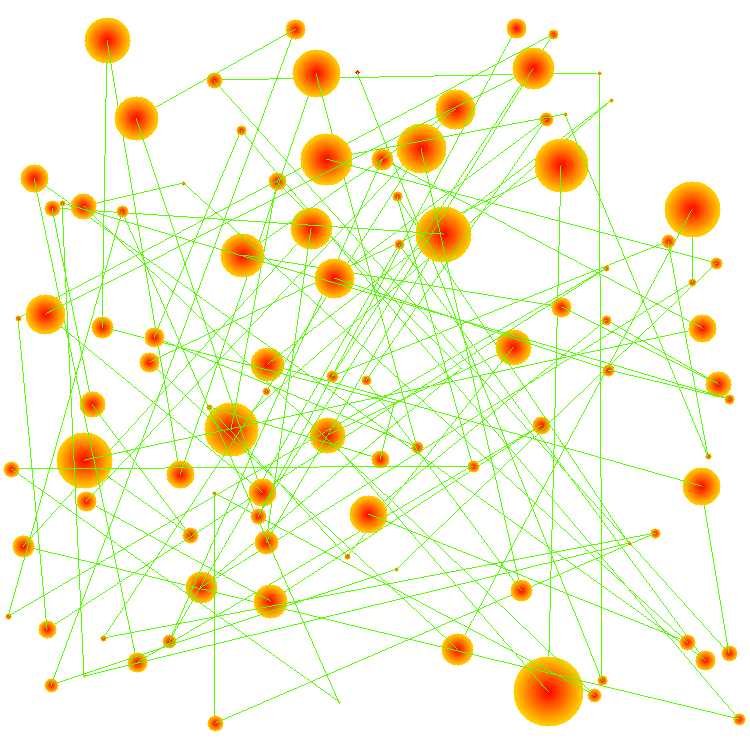

And this is what the traversal looks like on the mere 3 nodes found in the component of Directdebit:

Conclusion
Ultimately, we were able to come to the conclusion that wikipedia articles are very connected. Our most substantive proof of this is found from the usage of BFS in measuring the size of connected components. When it's taken into account that a staggering 99.65% percent of nodes can be found in one component, it becomes clear that these articles are almost all connected in some form or another. The articles that lie in the remaining 0.35% are ones that either have no links contained within them at all or link to articles that are extremely specific and don't have any branches (i.e Directdebit). Alongside BFS, Dijkstra's path finding algorithm helped us see that these articles were not connected by an overwhelmingly large distance, despite the size of their components. As described above, we found that we could connect any two articles (within a component) by going through no more than 5 links. This is especially remarkable when considering just how unrelated some of these articles are in nature.